En informatique, la performance est essentielle, avec une expérience utilisateur qui tient compte de la vitesse et de la gestion de la mémoire pour garantir le bon fonctionnement de l'application.
Imaginons un algorithme utilisé pour trier une liste d'objets, par exemple des billets de train. Si l'algorithme est capable de trier les billets rapidement mais nécessite une grande quantité de mémoire, il pourrait ne pas être le choix optimal pour un système avec des ressources limitées. Inversement, un algorithme qui utilise peu de mémoire mais prend beaucoup de temps pour trier pourrait ne pas convenir pour dans des situations où le temps est compté, comme les offres de dernière minute. Cette recherche d'équilibre est une constante en développement, aussi bien dans des domaines plus créatifs comme la conception de labyrinthes.
Dans cet article, nous allons aborder la notion de complexité algorithmique, un concept clé dans le monde de la programmation.
Qu’est-ce que la complexité algorithmique ?
En informatique, la complexité d'un algorithme correspond à la quantité de ressources nécessaires pour son exécution. Elle s'articule autour de deux aspects :
- la complexité temporelle, qui mesure la vitesse d'exécution d'un algorithme
- et la complexité spatiale, qui mesure la mémoire supplémentaire utilisée par un algorithme, en plus des données en entrée.
Ces complexités sont indépendantes. Pour un même algorithme, il est possible d'avoir une excellente complexité temporelle tout en ayant une complexité spatiale désastreuse, ou l'inverse.
Aussi, il est important de considérer comment un algorithme se comporte dans différents contextes d'utilisation. Cela signifie tester sa performance avec une variété d'entrées pour voir comment il réagit dans le meilleur des cas, le pire des cas et le cas moyen.
De manière générale, l'attention est portée sur la complexité dans le pire des cas pour préparer l'algorithme aux situations les plus difficiles, et sur la complexité moyenne, car elle représente le comportement habituel de l'algorithme. Dans notre exemple des billets de train, le pire scénario serait les billets triés dans l'ordre exactement inverse de celui souhaité tandis que le cas moyen serait les billets présents de manière aléatoire.
Si plusieurs algorithmes existent pour résoudre un même problème, calculer la complexité de chacun des algorithmes offre un moyen de comparer leur performance.
Comment calculer la complexité ?
Pour calculer la complexité, on utilise la notation Big O, de la forme O(f(n)). Elle permet d'exprimer la complexité d'un algorithme en fonction de la taille de l'entrée, généralement notée n. Le f(n) dans O(f(n)) représente ainsi une fonction mathématique qui décrit comment la complexité de l'algorithme croît avec n.
Lorsqu'on utilise la notation Big O, l'accent est mis sur le comportement des algorithmes à mesure que la taille de l'entrée devient très grande, donc pour de grandes valeurs de n.
Cette méthode écarte les éléments de moindre importance, comme les constantes et les termes mineurs, se concentrant sur le terme qui a le plus grand impact sur la croissance de la fonction. Par exemple, si la complexité exacte d'un algorithme est O(3n² + 5n + 7), on simplifie cela en O(n²), car pour de grandes valeurs de n, n² est le terme dominant.
La complexité temporelle va être calculée en regardant le nombre total d'opérations fondamentales effectuées par l'algorithme. Ces opérations incluent les comparaisons, les affectations, les accès à un tableau, mais aussi l'analyse des structures de contrôle telles que les boucles et les conditions.
Quant à la complexité spatiale, elle est déterminée en évaluant la quantité totale de mémoire requise par l'algorithme, qui peut inclure la mémoire pour les variables, les structures de données, et l'espace de pile pour les appels de fonction.
Cas pratique
Pour illustrer tout ça, revenons sur notre problème de billets. Voici un algorithme en Python qui va trier les billets par prix croissant.
def tri_insertion_par_prix(billets):
# Tri par insertion des billets de train en fonction du prix
for i in range(1, len(billets)):
billet_a_inserer = billets[i]
j = i - 1
# Comparer le prix du billet actuel avec ceux précédents
while j >= 0 and billets[j]['prix'] > billet_a_inserer['prix']:
billets[j + 1] = billets[j]
j -= 1
billets[j + 1] = billet_a_inserer
return billets
# Exemple d'utilisation
billets = [
{'destination': 'Paris', 'prix': 120},
{'destination': 'Nantes', 'prix': 90},
{'destination': 'Lille', 'prix': 110},
{'destination': 'Strasbourg', 'prix': 100},
{'destination': 'Bordeaux', 'prix': 80}
]
billets_tries = tri_insertion_par_prix(billets)
for billet in billets_tries:
print(billet)Dans la structure du code, nous observons une boucle for qui s'exécute n−1 fois, où n est le nombre de billets dans la liste. Imbriquée dans cette boucle for, se trouve une boucle while qui s'exécute un nombre variable de fois, dépendant de la position à laquelle le billet_a_inserer doit être inséré.
Dans le pire cas, où les éléments sont triés dans l'ordre inverse, la boucle while doit déplacer chaque billet trié jusqu'à présent pour insérer le nouveau billet au début de la liste. Pour le deuxième élément de la liste, la boucle while s'exécute une fois, pour le troisième élément deux fois, et ainsi de suite, jusqu'à ce que pour le dernier élément à insérer, elle s'exécute n−1 fois.
Le nombre total d'exécutions de la boucle while sur l'ensemble du tri est donc la somme d'une série : 1 + 2 + 3 + … + (n - 1). Cette somme est égale à (n × (n - 1))/ 2, ou autrement dit 1/2 n² - 1/2 n. On ne conserve que le terme dominant de cette fonction, ici n², et on trouve une complexité temporelle de O(n²), qui est en effet la complexité dans le pire des cas pour un tri par insertion.
La complexité spatiale est plus simple à calculer. Seules trois variables sont utilisées, deux entiers i et j pour les itérations ainsi que billet_a_inserer stockant temporairement un billet pendant que l'algorithme se déplace dans la liste. La taille en mémoire des trois éléments ne dépendent pas de la longueur de la liste de billets, c'est par conséquent un espace de stockage constant et la complexité spatiale du tri par insertion est de O(1).
Pour le meilleur et pour le pire
Maintenant que nous avons vu comment calculer des complexités, nous pouvons comparer et classer les algorithmes en fonction de leur efficacité. Connaître et comprendre les classes de complexité est important pour choisir le bon algorithme pour résoudre le problème. Voici les complexités les plus courantes :
- Complexité constante O(1) : Cette classe indique que l'algorithme exécute un nombre fixe d'opérations, ou s’exécute dans un temps constant, indépendamment de la taille de l'entrée. Un exemple typique est l'accès à un élément dans un tableau par son index.
- Complexité logarithmique O(log(n)) : Les algorithmes ayant une complexité logarithmique réduisent l'espace de problème à chaque itération. Par exemple, l'algorithme de recherche binaire divise par deux l'espace de recherche à chaque étape.
- Complexité linéaire O(n) : Cette catégorie indique que la quantité d'opérations réalisées ou le temps d'exécution augmentent de manière proportionnelle avec la taille des données d'entrée. La recherche linéaire est un exemple typique, nécessitant dans le pire des cas de parcourir la totalité de la liste pour trouver un élément.
- Complexité quasi-linéaire O(n ⋅ log(n)) : On retrouve dans cette classe quelques algorithmes de tri populaires, comme le tri rapide et le tri fusion. En moyenne, ils sont plus performants pour que le tri par insertion.
- Complexité quadratique O(n²) : Comme on l'a observé plus tôt, la complexité quadratique se manifeste dans les algorithmes où une boucle est imbriquée dans une autre, chaque boucle parcourant l'intégralité des données. La complexité quadratique fait partie de la complexité polynomiale, de la forme O(na) où a est un nombre entier.
- Complexité exponentielle O(2n) : Chaque élément supplémentaire dans les données d'entrée entraîne un doublement du nombre d'opérations et/ou du temps d’exécution. De manière générale, une complexité O(an) implique que chaque nouvel élément augmente les opérations ou le temps d'exécution d'un facteur de a. Un exemple classique d'algorithme à complexité exponentielle est l'implémentation naïve de la fonction qui génère un nombre de Fibonacci.
- Complexité factorielle O(n!) : Avec les algorithmes à complexité factorielle, chaque nouvel élément multiplie le nombre total d'opérations par le nombre d'éléments déjà présents. L'arrangement de différentes villes dans un itinéraire de voyage, en explorant tous les itinéraires possibles, est un exemple typique.
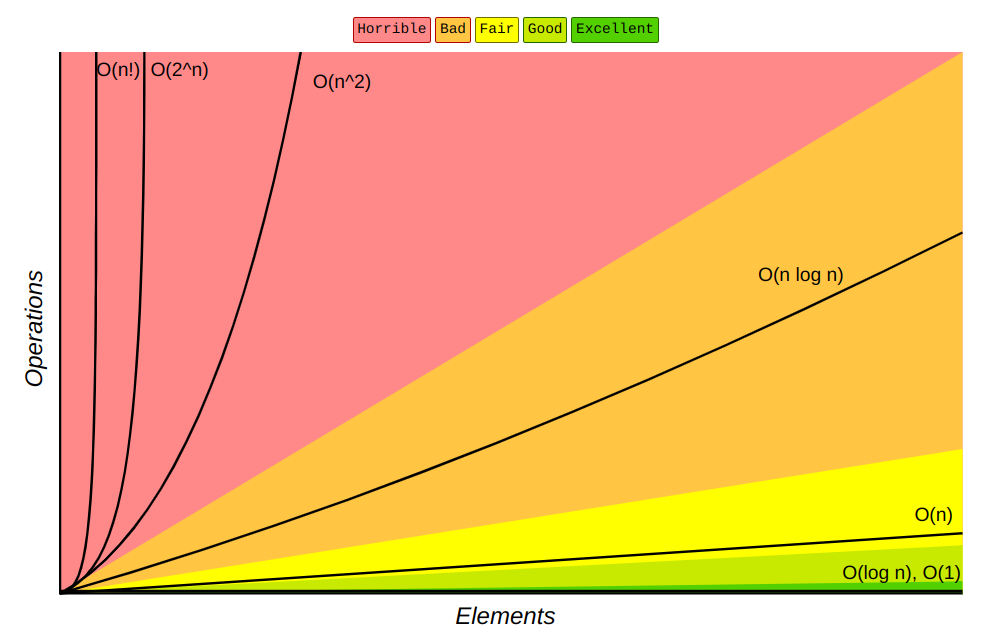
Le graphique ci-dessus montre le comportement des différentes complexités en fonction du nombre d'éléments en entrée. Il met en évidence l'efficacité des algorithmes à complexité logarithmique ou linéaire pour de grandes entrées, tandis que les complexités quadratique, exponentielle et factorielle deviennent rapidement impraticables à mesure que le nombre d'éléments augmente.
Cependant, les algorithmes à complexité quadratique ou exponentielle, ne sont pas nécessairement à bannir à tout prix. Dans des cas où la taille des données est relativement petite ou lorsque la complexité du problème à résoudre l'exige, ces algorithmes peuvent fournir des solutions exactes et optimales. Choisir le bon algorithme dépend de la taille des données mais aussi d'autres nombreux facteurs.
En conclusion
Ce voyage à travers la complexité algorithmique arrive à son terme. Identifier la complexité des algorithmes est une connaissance essentielle pour tout développeur, car elle permet de prendre des décisions pertinentes lors du développement. En vous armant de cette compréhension, vous êtes mieux préparé à créer des logiciels qui ne sont pas seulement fonctionnels, mais aussi optimisés pour les performances.
Maintenant que vous avez une base solide en complexité algorithmique, il est temps de mettre ces connaissances en pratique. Je vous propose quelques défis pratiques pour affûter vos compétences.