Soit vous ne savez pas quel restaurant choisir pour ce soir, soit vous n'arrivez pas à décider de qui va garder le chien après une douloureuse rupture : pierre, papier, ciseaux, c'est LA méthode efficace pour résoudre ce genre de problèmes. Pour ceux qui ont vécu dans une grotte ces dernières années, pierre-papier-ciseaux est un jeu qui consiste à sélectionner l'une des trois possibilités et à dévoiler le choix au même moment que votre adversaire. Les règles sont simples :
- La pierre bat les ciseaux.
- Les ciseaux battent le papier.
- Le papier bat la pierre.
Si l'on suit les lois de probabilité, il est évident que les chances de remporter la victoire, faire un match nul ou perdre sont toutes à une sur trois. Pourtant, grâce à l'apprentissage automatique, il est possible de modifier cette tendance — et peut-être garder le chien après tout.
Apprentissage automatique
L'apprentissage automatique (machine learning en anglais) est une branche de l'intelligence artificielle qui explique le processus qui permet à une machine d'apprendre à partir d'un ensemble de données pour ensuite être capable d'attribuer un chiffre ou une étiquette à une nouvelle donnée en imitant ce qu'un humain ferait.
L'apprentissage automatique est classé en trois catégories. La première est l'apprentissage supervisé où la machine utilise des données qui sont labelisées pour guider l'entrainement de la machine. La deuxième catégorie est l'apprentissage non supervisé : la machine est entrainée avec des données qui n'ont pas des étiquettes indiquant le résultat attendu. Elle doit se débrouiller pour les grouper par des caractéristiques similaires. Finalement, il existe l'apprentissage par renforcement, où la machine apprend à partir d'un système de récompenses au fil du temps.
Dans cet article, je vais utiliser la dernière approche car on souhaite prévoir le résultat de l'adversaire et agir en conséquence en mettant à jour l'apprentissage de la machine pendant chaque tour. Ainsi, si la machine réussi à prédire le coup adverse, je vais lui faire comprendre qu'elle a gagné avec une récompense. Si c'est le cas contraire, je vais plutôt lui indiquer qu'elle aurait dû choisir une autre option.
Chaînes de Markov
Andreï Markov, un mathématicien russe né en 1856 est reconnu pour ses nombreuses contributions dans le domaine scientifique, notamment dans la théorie des processus stochastiques. Son autre point fort : il savait bien jouer aux échecs. On s'intéresse surtout à lui grâce à un concept mathématique qui permet de prédire le futur : les chaînes de Markov.
L'idée derrière une chaîne de Markov est assez simple : la probabilité de l'événement suivant ne dépend que de l'état de l'événement actuel. Ce concept n'est valable que pour les processus qui respectent la propriété de Markov, c'est-à-dire, l'absence de mémoire. Cela se représente d'une façon mathématique comme suit :
\[\begin{gather*} \mathbb{P}(X_{t+1}=s|X_t=s_t, X_{t-1}=s_{t-1},\ldots, X_0=s_0)\\=\mathbb{P}(X_{t+1}=s|X_t=s_t) \end{gather*}\]
Je fais l'hypothèse que ceci est vrai pour le contexte du jeu. Ainsi, en considérant que la probabilité est la même pour chaque coup, la chaine de Markov de pierre-papier-ciseaux ressemble à ça :
Cela veut dire que si l'adversaire a joué pierre pendant le tour actuel, il y aura une probabilité de 1/3 qu'il choisira soit papier, soit ciseaux ou soit pierre au prochain tour. Les trois coups possibles comportent l'espace d'états et sont représentés de la manière suivante :
\[S=\{\textrm{pierre, papier, ciseaux}\}\]
Une trajectoire est l'ensemble d'états choisis à chaque tour. Prenons par exemple un utilisateur qui a fait cinq coups. Donc, pour aller de l'état \( \mathrm{pierre} \) au temps 0 vers l'état \( \mathrm{pierre} \) au temps 4, il a suivi une trajectoire \( \mathrm{pierre} \)-\( \mathrm{ciseaux} \)-\( \mathrm{ciseaux} \)-\( \mathrm{papier} \)-\( \mathrm{pierre} \).
\[\begin{align*}X_0 &=\textrm{pierre}, \\X_1 &= \textrm{ciseaux},\\X_2 &= \textrm{ciseaux},\\X_3 &= \textrm{papier},\\X_4 &= \textrm{pierre}\end{align*}\]
Chaque passage d'un état vers un autre est nommé transition. Elle est représentée par la matrice de transition qui contient les probabilités de passer d'un état au moment \( t \) vers un autre état au temps \( t+1 \) . Par exemple, dans la matrice suivante, supposons que l'adversaire vient de choisir \( \mathrm{pierre} \), il serait intéressant de savoir quelle est la probabilité qu'il choisira \( \mathrm{papier} \); si vous regardez la ligne de la \( \mathrm{pierre} \) et la colonne du \( \mathrm{papier} \), vous obtenez bien la valeur 1/3.
\[\def\interspace{6pt}\def\spacebefore{58pt}\begin{matrix}\hspace{\spacebefore}\begin{matrix} & X_{t+1} & \end{matrix} \\ \hspace{\spacebefore} \overbrace{\begin{matrix}\mathrm{pierre} &\mathrm{papier}&\mathrm{ciseaux}\end{matrix}}\\\begin{matrix}\\X_t\\ \\ \end{matrix}\left\{\begin{matrix}\mathrm{pierre}\\ \mathrm{papier} \\ \mathrm{ciseaux}\end{matrix}\right.\begin{pmatrix}\hspace{\interspace}1/3 \hspace{\interspace} & \hspace{\interspace} 1/3 \hspace{\interspace} & \hspace{\interspace}1/3 \hspace{\interspace}\\ 1/3 & 1/3 & 1/3 \\ 1/3 & 1/3 & 1/3 \end{pmatrix} \end{matrix}\]
Pourtant, l'information précédente n'est pas très utile pour prédire les coups de l'autre joueur. Alors, je vais faire une nouvelle hypothèse : l'adversaire ne s'ajuste pas aux probabilités précédentes et il a une tendance à choisir le prochain coup en lien avec le coup actuel. Il faudra dans ces conditions trouver les bonnes probabilités afin de prédire correctement ses choix. La matrice de transition d'un joueur serait biaisée comme dans cet exemple :
\[T=\begin{pmatrix}0 & 1/3 & 2/3 \\1/6 & 1/3 & 1/2 \\1/2 & 1/2 & 0\end{pmatrix}\]
J'ajoute encore un petit twist à cette formule. La matrice de transition représente la probabilité de \( n \) coups d'affilé au lieu d'un seul. Alors, considérons le cas de \( n=2 \) . Il y a trois états \( e \) : \( \mathrm{pierre} \) (\(R\)), \( \mathrm{papier} \) (\(P\)) et \( \mathrm{ciseaux} \) (\(S\)) et deux coups. Cela produit une matrice de taille \( e^n\times e \), c'est à dire, une matrice de \( 9\times3 \). Si vous utilisez trois coups, vous auriez une matrice de 81 éléments, avec quatre coups, la matrice aurait 243 éléments et si vous vouliez jouer la variation « pierre, papier, ciseaux, lézard, Spock » pour cinq coups, vous auriez 15.625 probabilités.
\[\def\interspace{4pt}\def\spacebefore{16pt}\begin{matrix}\begin{matrix}\hspace{\spacebefore}R & \hspace{\interspace}P & \hspace{\interspace}S\end{matrix}\\ \begin{matrix}RR\\RP\\RS\\PR\\PP\\PS\\SR\\SP\\SS\end{matrix}\begin{pmatrix}p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23}\\ p_{31} & p_{32} & p_{33}\\ p_{41} & p_{42} & p_{43}\\p_{51} & p_{52} & p_{53}\\p_{61} & p_{62} & p_{63}\\p_{71} & p_{72} & p_{73}\\p_{81} & p_{82} & p_{83}\\p_{91} & p_{92} & p_{93}\\\end{pmatrix}\end{matrix}\]
De cette manière-là, si l'adversaire a joué \( \mathrm{papier} \) (\(P\)) et \( \mathrm{pierre} \) (\(R\)) dans les deux coups précédents, il y a une probabilité \( p_{43} \) qu'il jouera \( \mathrm{ciseaux} \) (\(S\)) pour le prochain tour.
Mais bon, assez de maths pour aujourd'hui, passons directement aux choses sérieuses !
Algorithme Python
Pour cet exercice, j'ai utilisé Python 3.12.0. J'ai commencé par créer la classe MarkovChain qui contient un constructeur avec les paramètres labels (les étiquettes pour chaque type de coups, par exemple, R, P et S) et n_states (le nombre \( n \) de coups d'affilé qui seront considérés). Ce constructeur initialise la matrice de transition, un vecteur avec les coups réalisés par l'adversaire et aussi créé les étiquettes pour les coups précédents (pour \( n=2 \), RR, RP, RS, ... et SS).
import itertools
from random import randint
class MarkovChain:
def __init__(self, labels: list[str], n_states: int = 1):
# Initialiser l'objet en récupérant toutes les étiquettes
# possibles des coups précédents et en initialisant à 0
# la matrice de transition
self.n_states = n_states
self.labels = labels
self.prev_moves_labels = list(
map(''.join, itertools.product(labels, repeat=n_states)))
self.transition_matrix = [[0] * len(labels)
for _ in range(len(self.prev_moves_labels))]
self.opponent_history = []
J'ai ajouté la méthode updatequi enregistre le nouveau coup de l'adversaire dans la variable self.opponent_history. S'il y a assez de données, les derniers \( n \)coups sont récupérés et la matrice de transition est mise à jour.
def update(self, new_move):
# Mettre à jour la chaîne de Markov s'il y a suffisamment de données
if len(self.opponent_history) >= self.n_states:
prev_moves = self.opponent_history[-self.n_states:]
# Augmenter de 1 l'occurrence du nouveau coup
self.transition_matrix[self.prev_moves_labels.index(
''.join(prev_moves))][self.labels.index(new_move)] += 1
# Insérer un nouveau coup dans l'historique
self.opponent_history.append(new_move)
J'ai opté de ne pas utiliser les probabilités dans la matrice de transition, mais plutôt le nombre d'occurrences des événements. C'est-à-dire, une ligne qui aurait les probabilités ci-dessous :
\[ \begin{pmatrix}1/5 & 3/10 & 1/2 \end{pmatrix},\]
peut-être réécrite comme :
\[ \begin{pmatrix} 2 & 3 & 5 \end{pmatrix}\times 1/10.\]
Pourtant, j'ai négligé la constante qui multiplie la matrice n'étant pas si importante car l'événement le plus probable est celui qui a la valeur la plus élevée (5 dans l'exemple, le même cas que pour la probabilité 1/2) —il faut remarquer qu'au début, lorsque la matrice est initialisée à \( \begin{pmatrix}0 & 0 & 0\end{pmatrix} \), vous ne pouvez pas considérer celle-ci comme une matrice de transition puisque elle n'est pas conforme à la propriété selon laquelle la somme de chaque ligne est égale à 1.
Finalement, la fonction predict retourne le coup le plus probable en fonction des valeurs de la matrice de transition. S'il y a plusieurs coups équiprobables, cette fonction va renvoyer un parmi eux de manière aléatoire.
def predict(self):
# Renvoyer un mouvement aléatoire s'il n'y a pas suffisamment
# de mouvements précédents
if len(self.opponent_history) < self.n_states:
return self.labels[randint(0, len(self.labels) - 1)]
prev_moves = self.opponent_history[-self.n_states:]
# Récupérer tous les indices qui ont le maximum d'événements
occurrences_for_move = self.transition_matrix[
self.prev_moves_labels.index(''.join(prev_moves))]
indexes = [i for i in range(0, len(occurrences_for_move))
if occurrences_for_move[i] == max(occurrences_for_move)]
# Obtenir un coup gagnant en prédisant le jeu de l'adversaire
# Renvoyer un choix aléatoire s'il y a deux mouvements avec la même
# probabilité
opponent_move_prediction = self.labels[
indexes[randint(0, len(indexes) - 1)]]
return opponent_move_prediction
Vous pouvez jeter un coup d'œil à l'implémentation de cet algorithme ici.
Et si vous souhaitez allez plus loin, découvrez l'article de mon collègue Alexandre sur comment "comprendre la complexité des algorithmes".
Résultats
J'ai testé cet algorithme avec cinq collègues chez SFEIR Strasbourg. La méthodologie consistait à jouer cent fois contre la machine (une chaîne de Markov à deux états) et voir qui remportait le plus de victoires. Voici les résultats :
| Joueur | Victoires | Nuls | Défaites | Taux de victoire du joueur | Taux de victoire de la machine |
|---|---|---|---|---|---|
| 1 | 27 | 34 | 39 | 40,91% | 59,09% |
| 2 | 32 | 30 | 38 | 45,71% | 54,29% |
| 3 | 25 | 35 | 40 | 38,46% | 61,54% |
| 4 | 28 | 16 | 56 | 33,33% | 66,67% |
| 5 | 26 | 21 | 53 | 32,91% | 67,09% |
| Total | 138 | 136 | 226 | 37,91% | 62,09% |
Les cents coups réalisés par les joueurs ont été enregistrés et je les ai utilisé après pour jouer encore contre la machine. Pourtant, cette fois-ci, j'ai modifié le nombre d'états à utiliser par l'algorithme en le variant de 1 à 5.
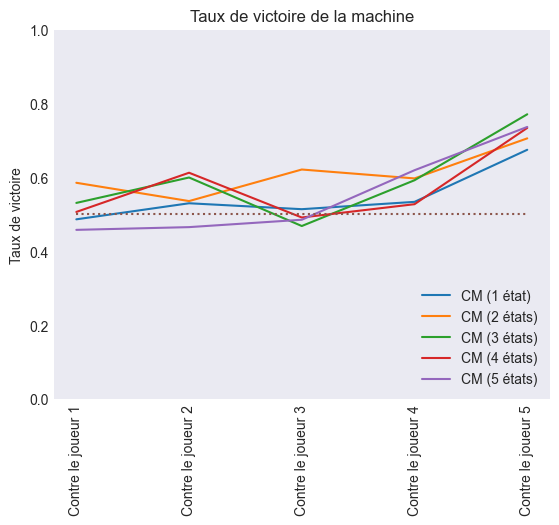
J'ai comparé les cinq méthodes pour déterminer laquelle avait le taux de victoire le plus élevé et il a été évident que la chaîne de Markov à deux états remportait la palme.
| Nombre d'états | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Taux de victoire | 55,00% | 61,32% | 60,22% | 57,93% | 55,52% |
Ensuite, j'ai confronté cette solution à une machine qui ne faisait que des coups aléatoires. Voici les résultats :
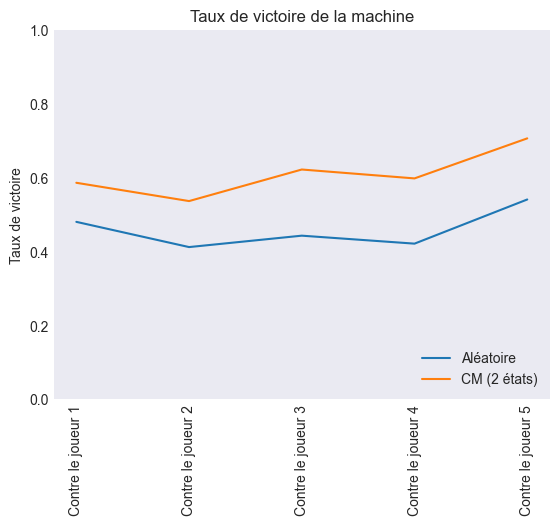
Conclusion
Il est clair que l'apprentissage automatique est un outil intéressant pour améliorer les performances dans un jeu qui semble régi par le hasard. Un algorithme basé sur le concept probabiliste des chaînes de Markov a permis à une machine d'obtenir 62,09% des victoires contre des joueurs humains.
Cependant, il est important de dire que la méthode abordée dans cet article est l’une des plus simples dans le domaine de l’intelligence artificielle. Des alternatives telles que les réseaux de neurones restent à examiner. Je vous encourage donc à continuer d’explorer le monde de l’intelligence artificielle et de découvrir l’éventail de solutions qu’elle peut apporter à notre quotidien.
Si vous souhaitez consulter d'autres ressources, il y a des sites comme RPSContest.com ou Kaggle où des différents algorithmes s'affrontent pour gagner à pierre-papier-ciseaux. Il existe également le site Web de l'Université de Stirling où vous pouvez jouer en ligne contre une machine. La certification freeCodeCamp vous permet de tester vos connaissances.
Remerciements
Je tiens à remercier Matthieu Cavalier, Louis Pascuzzi, César Velásquez, Théophile Montémont et Théo Genez qui m'ont aidé à la réalisation de cet article.








