Aujourd'hui, on parle de plus en plus de physique quantique, d'informatique quantique, d'ordinateurs quantiques ou de programmation quantique. Le sujet anime parfois les débats les plus fous : le chat de Schrödinger est-il vivant ou mort ?
- Certains diront peut-être "vivant" et ils auront peut être raison.
- D'autres diront peut-être "mort" et ils auront également peut-être raison.
- D'autres encore diront qu'il est mort-vivant, bon ok, ceux-là auront tort.
- Enfin les derniers diront qu'il est à la fois vivant et mort. Euuh... non, rien n'est "à la fois vivant et mort". En revanche cela aide notre esprit à mieux se représenter les choses.
Cet article permettra de rendre les notions de base plus claires, pour ensuite présenter le framework Strange et montrer à travers de quelques exemples comment il permet de les mettre en place.
Concepts de base
Le spin
Le spin est la notion élémentaire sur laquelle se base la programmation quantique. Lorsqu'on parle de "bit quantique" (ou qubit), le spin est la propriété physique permettant de donner sa valeur au bit quantique. Mais qu'est-ce donc d'un point de vue physique ?
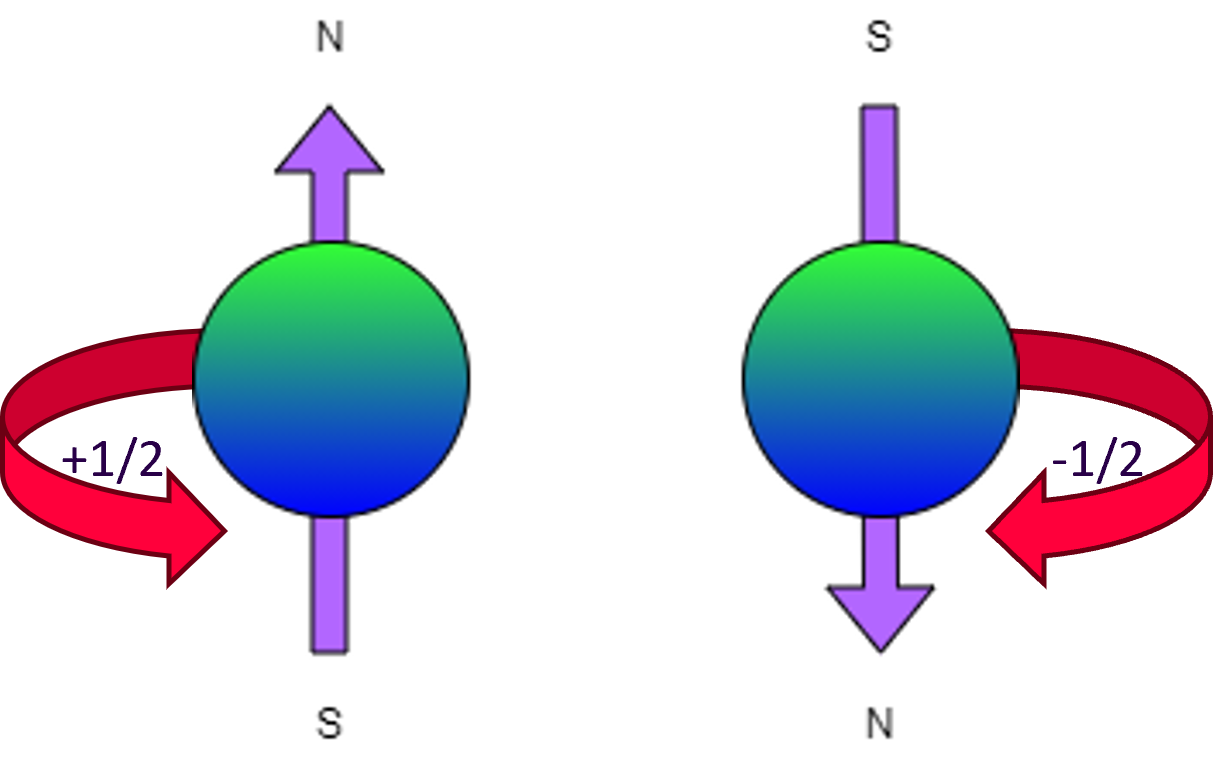
Il s'agit d'une propriété discrète des particules. Dans le cas des électrons, cette propriété peut valoir +1/2 ou -1/2. On représente souvent le spin comme le sens de rotation des particules, bien que le spin ne soit pas le sens de rotation d'une particule. Il s'agit simplement d'une facilité de représentation.
La superposition quantique
Tant qu'on n'a pas observé le spin d'une particule, il est impossible de savoir sa valeur. En revanche, la probabilité d'observer telle ou telle valeur est connue. Dans la suite, nous simplifierons en supposant que cette probabilité est de 50%.
La superposition quantique est simplement l'expression du fait que tant que nous n'observons pas une propriété quantique, nous ne connaissons que sa probabilité. Le spin n'est pas égal à +1/2 ET -1/2, mais on peut dire qu'il est égal (par représentation) à 50% +1/2 et 50% -1/2.

Le chat de Schrödinger est bien soit mort, soit vivant, mais tant que nous ne l'observons pas, la superposition quantique permet de nous le représenter :
- Mort : 50%
- Vivant : 50%.
C'est en cela que l'observation altère cet état quantique : quand nous observons le chat, s'il est vivant, il le "devient" à 100%.
L'intrication
On dit que deux particules sont intriquées lorsque leur état est synchronisé. Cela signifie que lors de l'observation des particules, leur état sera exactement le même. En programmation quantique, cela signifie que deux qubits intriqués auront la même valeur. Attention cependant : l'intrication ne garantit pas que le changement d'état d'une particule implique le changement d'état de l'autre particule. En d'autres termes, deux particules peuvent être "désintriquées".

Quelques portes quantiques
La porte quantique Pauli-X
Cette porte permet simplement d'inverser la valeur d'un qubit. La probabilité d'obtenir "1" lors de l'observation sera alors inversée.

La classe représentant cette porte en Strange est simplement nommée "X". Son constructeur prend en paramètre un entier permettant d'identifier le qubit sur lequel appliquer cette porte.
var xGate = new X(3);
La porte quantique Hadammard
Cette porte engendre un état de superposition quantique sur un qubit. Le qubit aura alors autant de chance de valoir 0 ou 1 lors de son observation.

La classe représentant cette porte en Strange est simplement nommée "H". Son constructeur prend en paramètre un entier permettant d'identifier le qubit sur lequel appliquer cette porte.
var hadammardGate = new H(3);
⚠ Tant que cette porte n'a pas été appliquée à un qubit, on considère que sa valeur est de 0 (équivalent à un bit classique de valeur 0).
La porte quantique CNot
Cette porte prend en paramètre 2 qubits : un qubit de contrôle et un qubit cible. Elle inverse l’état d’un qubit cible si le qubit de contrôle est à 1 et ne fait rien sinon.
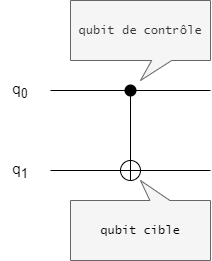
La classe représentant cette porte en Strange est nommée "Cnot". Son constructeur prend en paramètre deux entiers permettant d'identifier respectivement le qubit de contrôle et le qubit cible.
var cNotGate = new Cnot(1,2);
Exemple de l'intrication quantique
Objectif
On souhaite mettre en place un circuit quantique qui implémente l'intrication. La définition de l'intrication que nous souhaitons mettre en place est la suivante : deux qubits sont intriqués si et seulement si ils sont dans un état de superposition quantique et lors de l'observation, leur mesure est garantie identique.
Circuit quantique
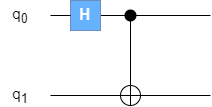
Le circuit se lit de gauche à droite.
- Au début, q0 et q1 valent 0
- La porte Hadammard est appliquée à q0, ce dernier passe donc en état de superposition quantique.
- La porte CNot est appliquée sur (q0,q1).
- Cette porte n'a pas d'effet de modification sur q0. En revanche elle va lire son état.
- Si la mesure de q0 est 0 alors CNot n'a pas d'effet sur q1 et la mesure de ce dernier restera 0. Dans ce cas, q0 et q1 auront donc la même mesure.
- Si la mesure de q0 est 1 alors CNot inversera la mesure de q1 qui passera donc de 0 à 1. Une fois encore, q0 et q1 auront la même mesure.
Implémentation
public void intrication(){
// définition d'un circuit quantique avec 2 qubits
Program program = new Program(2);
// 1ère étape : application de Hadamard sur q0
Step step0 = new Step();
step0.addGate(new Hadamard(0));
program.addStep(step0);
// 2ème étape : application de CNot sur (q0,q1)
Step step1 = new Step();
step1.addGate(new Cnot(0,1));
program.addStep(step1);
// Défintion de l'environnement d'execution : simulateur
QuantumExecutionEnvironment environment =
new SimpleQuantumExecutionEnvironment();
// Execution du programme et lecture des résultats
var results = environment.runProgram(program);
Qubit[] qubits = result.getQubits();
int measureQ0 = qubits[0].measure();
int measureQ1 = qubits[1].measure();
LOGGER.info(STR."(\{measureQ0},\{measureQ1})");
}
Conclusion
Au travers de cet article, une brève introduction à la programmation quantique a été faite à travers du framework Strange. Il existe plusieurs autres technologies (par exemple Q#) avec le même objectif : écrire des algorithmes quantiques.
Pour plus d'informations sur le framework Strange









